반응형
갑자기 궁금해져서 인터넷을 검색해봤는데, 자료를 찾을수가 없네요.
가만히 생각을 해보니 첫번째 9개칸에서 9*8*7*6*5*4*3*2*1 의 경우의 수가 생기고,
다음칸부터는 조금씩 줄어들것같고, 마지막 9개같은 자동적으로 결정이 될것같은데,
어떻게 계산식을 산출하는지 확률 공부한지가 오래되서 도무지 모르겠네요...-_-;;
혹시 수학적으로 어떻게 계산을 하는지 아시면 답변 좀 부탁드리겠습니다.
가만히 생각을 해보니 첫번째 9개칸에서 9*8*7*6*5*4*3*2*1 의 경우의 수가 생기고,
다음칸부터는 조금씩 줄어들것같고, 마지막 9개같은 자동적으로 결정이 될것같은데,
어떻게 계산식을 산출하는지 확률 공부한지가 오래되서 도무지 모르겠네요...-_-;;
혹시 수학적으로 어떻게 계산을 하는지 아시면 답변 좀 부탁드리겠습니다.

궁금해서 위와 같이 질문을 했더니 제대로된 이야기는 없이 6670903752021072936960개가 있다는 댓글이...
저 숫자만을 가지고 검색을 해보니
9!*2^13*3^4*27704267971 = 6.67e21 = 6670903752021072936960 라고 66해 7090경...-_-;;
http://www.afjarvis.staff.shef.ac.uk/sudoku/
http://polly97.wordpress.com/2007/06/13/
이중에서 대칭이나 회전등을 통한 중복되는 경우들을 제외한 스도쿠 퍼즐은 모두 5,472,730,538 가지라고...
http://www.why.is/svar.php?id=7220
There is no known formula for the number of Sudoku grids on a n×n board. Sudoku grids are a special case of what are termed "Latin squares". These squares/grids, even though having a simple definition, are not easily attacked using the standard techniques of enumeration. Many problems in combinatorics suffer from this problem, however it does not mean that we cannot study properties of these objects.
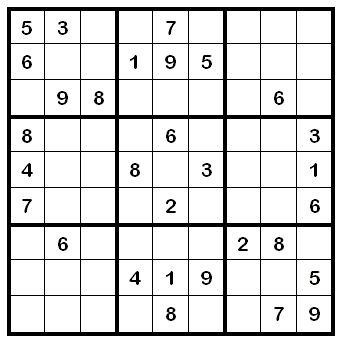
The reason for this is the freedom in producing a valid Sudoku board. In order to make such a board, one must check that each of the 27 sub-configurations (these include all rows, columns and 3*3 blocks) are permutations of {1,2,3,4,5,6,7,8,9}. When producing an exact formula is not possible, mathematicians sometimes resort to giving upper and lower bounds on the number of configurations.
The question concerning the number of different Sudoku's is even harder to answer! In problems of this type it is not immediately clear how to decide when two Sudoku grids are the same. If one rotates a Sudoku grid by 90 degrees then it is easy to see that nothing has changed. If one flips such a grid upside down then, again, it is essentially the same.
However, if one changes each of the numbers 1,2,3,4,5,6,7,8,9 to the numbers 5,8,3,2,6,9,1,4,7 then is it the same? Well, even though this may be less obvious than the other operations, yes of course. From the initial values that one is given, exactly the same reasoning is used to complete the board. There are several other similar operations that one can also do to make a new grid that looks different but is essentially the same.
These operations define what is termed a group in mathematics. Let us call this group G. In order to find the number of different boards, one checks the list of all the configurations on a 9×9 board, looks at the board produced by each of the transformations in the group: if it is already listed then remove it. This will produce a list of all the different Sudoku's on a 9×9 board.
To be more exact, let S be the list of ALL Sudoku's on a 9×9 grid and let L be the empty list. For each grid s in S, if g(s) is in L for some group element g then we do not add s to the list L. Otherwise we add it. Once this has been done for all grids in S we will have a list of different grids L.
The number of these was determined by Russel and Jarvis to be 5,472,730,538.
People interested in the number of particular games, configurations et cetera should look at Neil Sloane's wonderful On-line Encyclopedia of Integer Sequences.
Picture: The original question was as follows:
Question
How many different Sudoku's is it possible to make?
Asked By
Kristján Júlíusson
Answer
The number of Sudoku grids on a 9×9 board is 6,670,903,752,021,072,936,960. This number is given in Felgenhauer and Jarvis' article Enumerating possible Sudoku grids. To calculate this number the authors first made several observations on the configurations that needed to be checked, and then used a computer to find those configurations that produced a valid Sudoku grid.There is no known formula for the number of Sudoku grids on a n×n board. Sudoku grids are a special case of what are termed "Latin squares". These squares/grids, even though having a simple definition, are not easily attacked using the standard techniques of enumeration. Many problems in combinatorics suffer from this problem, however it does not mean that we cannot study properties of these objects.

The reason for this is the freedom in producing a valid Sudoku board. In order to make such a board, one must check that each of the 27 sub-configurations (these include all rows, columns and 3*3 blocks) are permutations of {1,2,3,4,5,6,7,8,9}. When producing an exact formula is not possible, mathematicians sometimes resort to giving upper and lower bounds on the number of configurations.
The question concerning the number of different Sudoku's is even harder to answer! In problems of this type it is not immediately clear how to decide when two Sudoku grids are the same. If one rotates a Sudoku grid by 90 degrees then it is easy to see that nothing has changed. If one flips such a grid upside down then, again, it is essentially the same.
However, if one changes each of the numbers 1,2,3,4,5,6,7,8,9 to the numbers 5,8,3,2,6,9,1,4,7 then is it the same? Well, even though this may be less obvious than the other operations, yes of course. From the initial values that one is given, exactly the same reasoning is used to complete the board. There are several other similar operations that one can also do to make a new grid that looks different but is essentially the same.
These operations define what is termed a group in mathematics. Let us call this group G. In order to find the number of different boards, one checks the list of all the configurations on a 9×9 board, looks at the board produced by each of the transformations in the group: if it is already listed then remove it. This will produce a list of all the different Sudoku's on a 9×9 board.
To be more exact, let S be the list of ALL Sudoku's on a 9×9 grid and let L be the empty list. For each grid s in S, if g(s) is in L for some group element g then we do not add s to the list L. Otherwise we add it. Once this has been done for all grids in S we will have a list of different grids L.
The number of these was determined by Russel and Jarvis to be 5,472,730,538.
People interested in the number of particular games, configurations et cetera should look at Neil Sloane's wonderful On-line Encyclopedia of Integer Sequences.
Picture: The original question was as follows:
How many different Sudoku's is it possible to make (in the usual size 9x9, as in most newspapers) - and how do you calculate that?
반응형
'자료 iN ' 카테고리의 다른 글
| 하나은행- 금융거래 일시 중단 안내 (5/1-5/4) (0) | 2009.04.13 |
|---|---|
| 1박2일에 나온 캠핑용품 투버너 (0) | 2009.04.13 |
| 자전거 튜브 벨브의 종류와 펌프 고르기 (0) | 2009.04.09 |
| 2009 여의도 벚꽃 축제에서 불꽃축제를! (0) | 2009.04.08 |
| 편리한 홈택스! 양도세도 자동계산 해드려요! - 절세전략 완전정복! (0) | 2009.04.08 |


